I wrote the last question in the 2023 NAC, called Finding Friends. The premise of the question is that there is an astronomer named Andrew trying to chase a star $\chi$, and the task is to compute some interesting metrics related to whether or not he will ever be able to catch $\chi$.

The original problem was very long, and the final version that ended up being in the exam was condensed by a few parts in order to not make the exam too long or impossible. I figure there is no better place to dump the entire question than my blog, so here is the entire question and solution that I originally submitted.

Question: Finding Friends (solution)

In the future, Earth is perfectly spherical and completely covered with water. Sailor Andrew is on a boat initially positioned at the equator in such that a way that $\gamma$, the vernal equinox, is directly overhead. He observes a star $\chi$ with right ascension and declination $(\alpha, \delta)=(15^{\circ}, 10^{\circ})$. He wants to chase $\chi$, and he needs your help.

You may assume the following numerical values for each constant:

• $R_{\oplus}$ is Earth’s radius (same as the current day value).
• $\omega = 2\pi/(24\text{ hrs})$ is Earth’s angular frequency.
• His boat is very fast; its maximum speed is $\vert v\vert = \omega R_{\oplus}/4$.
• The vernal equinox $\gamma$ has celestial coordinates $(0^{\circ}, 0^{\circ})$.
• $(\alpha, \delta) = (15^{\circ}, 10^{\circ})$.

Section 1

(a): 2 points (sol)

Calculate the angular distance between $\gamma$ and $\chi$. Express your answer in degrees.

In his starting position, $\chi$ is somewhere above his horizon. As he sails to different parts of the planet and time passes, $\chi$ moves around his night sky. He wants sail his boat in order to get $\chi$ as close to his zenith as possible. To make sure he is as efficient as possible, he wants to make a few calculations first.

(b): 2 points (sol)

If he does not move his boat from his starting position, calculate the minimum zenith distance that $\chi$ reaches. Express your answer in degrees.

Now, he considers what would happen if he sails straight north at all times.

(c): 3 points (sol)

Starting from his intial position when $\gamma$ is overhead, he directs his boat straight north and starts sailing with speed $\vert v\vert$. Does $\chi$ first cross his north-south meridian or east-west meridian? Briefly explain why this is the case.

(d): 3 points (sol)

Calculate the zenith distance of $\chi$ when it first crosses his north-south meridian. Express your answer in degrees.

(e): 15 points (sol)

Calculate the zenith distance of $\chi$ when it first crosses his east-west meridian. Express your answer in degrees.

Let $X$ be the point in his trajectory (in the celestial sphere) at which $\chi$ reaches its minimum zenith distance, and $N$ be the north celestial pole. Note that $X$ is a point in the celestial sphere, and not Earth.

(f): 6 points (sol)

Argue that $\angle N\gamma X+\angle \chi XN \approx \pi/2$, where both angles are spherical angles. Then, calculate $\angle \chi XN$. Express your answer in degrees.

Note: For this part only, you may assume that the declination of $X$ is small, hence the approximation.

(g): 15 points (sol)

Calculate the minimum zenith distance that $\chi$ reaches. Express your answer in degrees.

For this problem:

• You may no longer assume that the declination of $X$ is small. However, you may use the value of $\angle{\chi XN}$ derived in part (f).
• You are given that the right ascension of $X$ is within $(\alpha\pm 2^{\circ})$.
• His trajectory in the celestial sphere is not necessarily a great circle. Be careful when computing angles and lengths!

Section 2

His next consideration is to see what happens if he steers his ship directly towards $\chi$ at all times. As before, assume he starts from his initial position with $\gamma$ overhead, and his boat always moves with speed $\vert v\vert$. If $\chi$ passes below his horizon, he stops his ship.

As before, assume he starts from his initial position when $\gamma$ is overhead. Provide a brief argument for why this steering strategy will take him at least one day (i.e., $2\pi/\omega$) until he can get $\chi$ directly overhead using this method.

Relative to the celestial sphere, he has two velocities: one due to the rotation of earth, $v_r$, and one due to his boat’s velocity, $v$. Let $\zeta$ be the counterclockwise angle from $v_{r}$ to $v$. Let $\theta$ be the counterclockwise angle from $v_{r}$ to $v_t$, where $v_t$ is his net velocity in the celestial sphere.

Now we will attempt to characterize how the zenith distance changes over his trajectory. At any particular point in his path, let $\phi$ be his latitude.

(h): 2 points (sol)

Find an expression for $\tan \theta$ in terms of $\zeta$, $v$, $\omega$, $R_{\oplus}$, and $\phi$. Some of these constants have known numerical values, but you do not have to substitute them in.

(Hint: Consider the components of $v_t$. Your final expression should involve all the listed constants.)

(i): 7 points (sol)

In his current trajectory, prove that a small change in the zenith distance of $\chi$, $\Delta z$, corresponds to a horizontal displacement in the celestial sphere by an angle of

Note that $\Delta z$ and $\Delta \lambda$ are small angular changes.

(j): 6 points (sol)

As before, assume that he starts with $\gamma$ overhead and steers his boat towards $\chi$ at all times. At some point before $\chi$ dips below the horizon for the first time, it reaches a minimum zenith distance. At this moment in time, compute $\cos{\phi}\sin{\theta}$. Your answer should be numerical.

(Hint: you may find your expression from part (h) useful.)

Section 3

He is not satisfied with these results. He feels there should be an optimal way to get $\chi$ directly overhead, as fast as possible. Help him figure out the fastest way to get $\chi$ to his zenith.

(k): 2 points (sol)

Given that he is allowed to maneuver his boat however he wants throughout the duration of his journey, and that he starts from his initial position with $\gamma$ overhead, show that $\chi$ cannot be at his zenith the first time it culminates, i.e., crosses his north-south meridian.

(l): 7 points (sol)

Let $t$ be the fastest time he can get $\chi$ to his zenith. Compute the quantity $(t-\text{20 hrs})$, in seconds.

Solution: Finding Friends (question)

Section 1

(a) (ques)

Let $N$ be the north celestial pole and $d$ be our desired distance. Then, the spherical law of cosines in $\triangle{N\gamma\chi}$ gives

which implies $d = \arccos{(\cos{\delta}\cos{\alpha})}\approx 17.96^{\circ}$.

(b) (ques)

Since $\chi$ is to his east, it has not yet culminated. Also, since he is not moving, $\chi$ achieves its minimum zenith distance as it culminates.

One way to figure out this minimum zenith distance is to consider the view from his horizon. $\chi$ moves through the small circle representing the declination line at $\delta$. Since he is located on the equator, the celestial equator from his perspective passes through the zenith. Therefore, the minimum zenith distance is the distance between the declination line at $\delta$, and the celestial equator, which is $\delta = 10^{\circ}$.

An alternative approach is to consider his movement through the celestial sphere. Culmination occurs when his location and $\chi$ have the same right ascension. At this point, their distance is $\delta$, so this is the minimum zenith distance.

(c) (ques)

$\chi$ starts in the northeastern quadrant of the sky. When $\chi$ crosses the north-south meridian, it changes from the east to west hemisphere. When $\chi$ crosses the the east-west meridian, it changes from the north to south hemisphere.

At time $t$, his location in the celestial sphere is given by $(\omega t, \omega t/4)$, so $(\alpha, \alpha/4)$ is a point in his trajectory. Since $\alpha/4 < \delta$, $\chi$ culminates in his northern sky. Thus, $\chi$ passes the north-south meridian before passing the east-west meridian.

(d) (ques)

$\chi$ culminates when it has the same right ascension as Andrew, so $\omega t = \alpha$. So, the zenith distance is given by

(e) (ques)

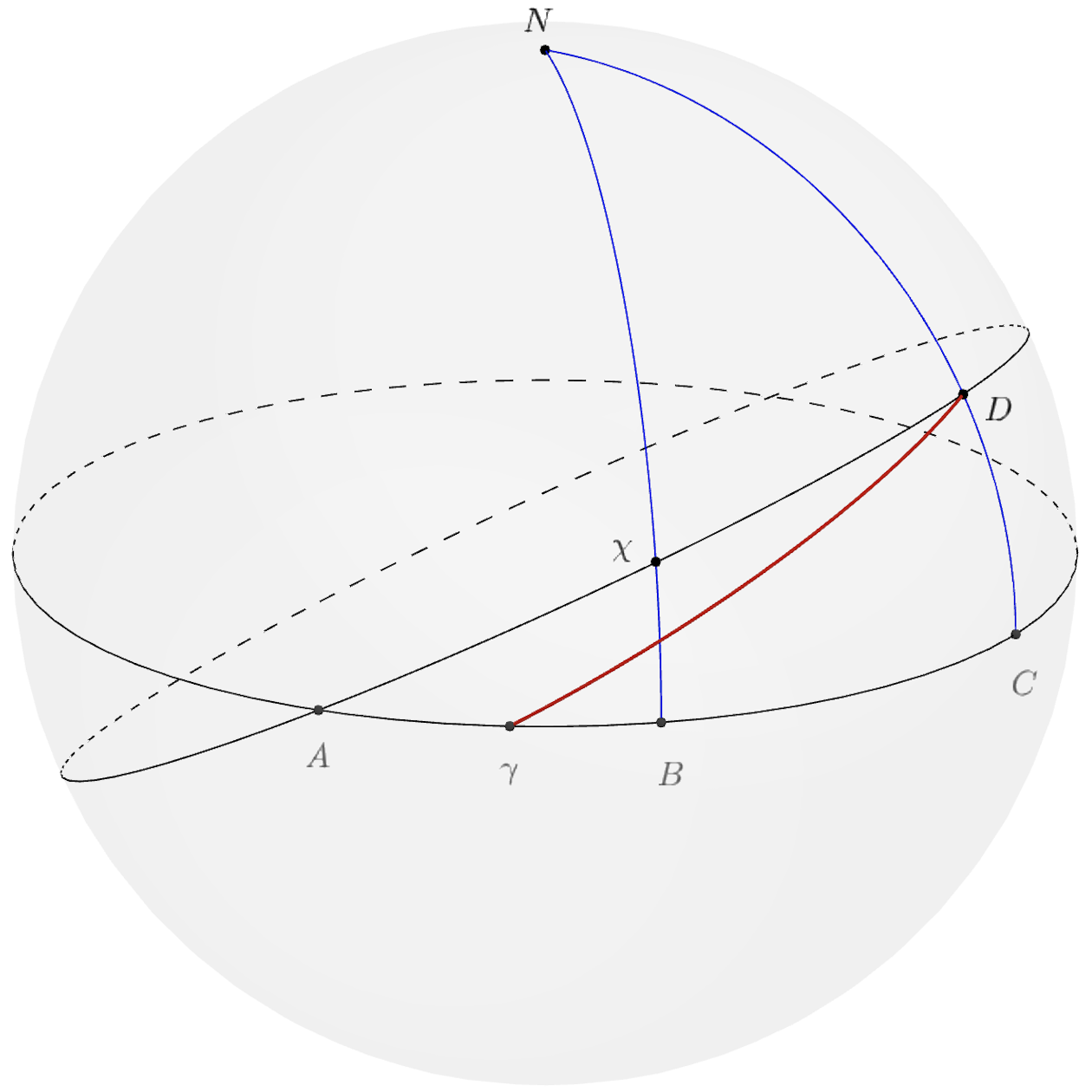
Let $D$ be his position in the celestial sphere. When $\chi$ first crosses the east-west meridian, $D$ must satisfy $\angle ND\chi = 90^{\circ}$, as shown in the diagram below. The red line in the diagram represents his trajectory in the celestial sphere (this trajectory is not a great circle, so we cannot use it in our calculations).

Now, chasing angles:

• The perpendicular condition implies that $D$ is the apex of another great circle (call $\Gamma$) that passes through both $D$ and $\chi$. $\Gamma$ intersects the equator at a point $A$, such that $DA = 90^{\circ}$.
• As labelled in the diagram, let $B$ and $C$ be the feet of $\chi$ and $D$ from $N$, respectively (so that $\angle \chi BA = \angle DCA = 90^{\circ}$). Since $D$ is the apex of $\Gamma$, $DA = CA = 90^{\circ}$.
• We know $\gamma B = \alpha$ and $\gamma C = \omega t$, so $AB = 90^{\circ}+\alpha-\omega t$.
• We also know that $\chi B = \delta$, and $DC = \omega t/4$.

Our goal is to find the zenith distance, which is $\chi D$. To find this arc, we’ll need $\omega t$, which will let us solve for the right ascension of $D$. Let $\varepsilon = \angle{\chi AB} = \angle{DAC}$. The four-parts formula in both $\triangle{\chi AB}$ and $\triangle{DAC}$ gives

Substituting known values, this reduces to the equation

We can use this to numerically iterate for $\omega t$. Our initial guess does not need to be good; any value from around $10^{\circ}$ to $70^{\circ}$ converges in a few iterations, giving us $\omega t\approx 46.97^{\circ}$.

Finally, a few more angles:

• $\angle \chi ND = \angle BNC = \omega t - \alpha$.
• $N\chi = 90^{\circ}-\delta$.
• $ND = 90^{\circ} - \omega t/4$.

These are all known values. The spherical law of cosines in $\triangle{N\chi D}$ now gives

(f) (ques)

The zenith distance $\chi X$ is minimized when $\angle \chi X\gamma = 90^{\circ}$. Let $X'$ be the foot of $X$ from $N$, so that $\angle NX'\gamma = 90^{\circ}$. Then, if we let $\beta = \angle NX\chi$:

• $N, X, X'$ lie on the same great circle, $\angle NX\chi + \angle \chi X\gamma + \angle \gamma X X' = 180^{\circ}$, which implies $\angle \gamma XX' = 90-\beta$.
• Since the latitude of $X$ is small, and $\triangle{XX'\gamma}$ is right, we can say that $\angle \gamma XX' + \angle X\gamma X'\approx 90^{\circ}$, so $\angle X\gamma X' \approx \beta$. This approximation is valid since $\gamma X' = \omega t = 4X'X$, so $\triangle{XX'\gamma}$ can be approximated by a flat right triangle.
• Since $\angle N\gamma X' = 90^{\circ}$, $\beta$ and $\angle N\gamma X$ add to $90^{\circ}$, as desired.

To compute $\beta$, we can use our approximation of $\triangle{XX'\gamma}$ as a flat right triangle to say that $\tan{\beta}\approx 1/4$, so $\beta\approx 14^{\circ}$.

(g) (ques)

Consider $\triangle{NX\chi}$. We know the lengths of two sides, $N\chi = 90^{\circ}-\delta$ and $NX = 90^{\circ}-\omega t/4$, and the values of a nested and adjacent angle, $\angle N = \omega t-\alpha$ and $\angle X = \beta$. We want to find the length of the zenith angle, which is $X\chi$. Unfortunately, we can’t directly solve for $X\chi$, but we may first try solving for $\omega t$ using the information we already have, which will give us enough information about the triangle to solve for $X\chi$.

Applying the four parts formula:

As in part (e), we can isolate $\omega t$ and try to solve this equation with numerical iteration:

Unfortunately, this diverges for most values. Luckily, we’re given that $\omega t$ is within $(\alpha\pm 2^{\circ})$, which is a good enough range for us to still find a solution at $\omega t\approx 16.45^{\circ}$.

Finally, the law of sines in $\triangle{X\chi N}$ gives

Section 2

(h) (ques)

The vertical component of $v_t$ is given by $v\sin{\zeta}$, while the horizontal component is given by $v\cos{\zeta} + \omega R_{\oplus}\cos{\phi}$. Therefore,

(i) (ques)

The key for this part is to draw good diagrams. Below is a larger picture of the trajectory:

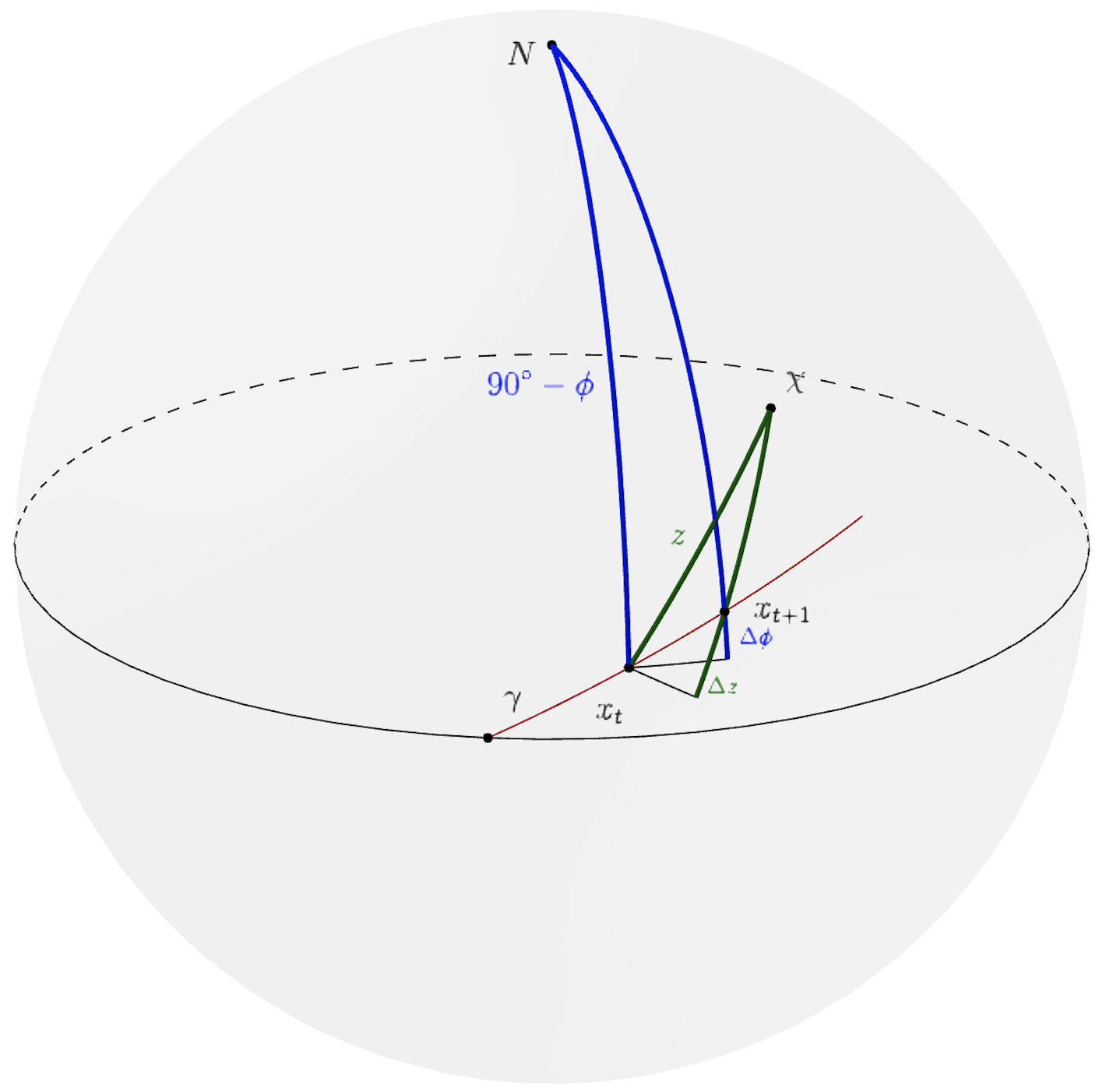
Below we decompose the trajectory:

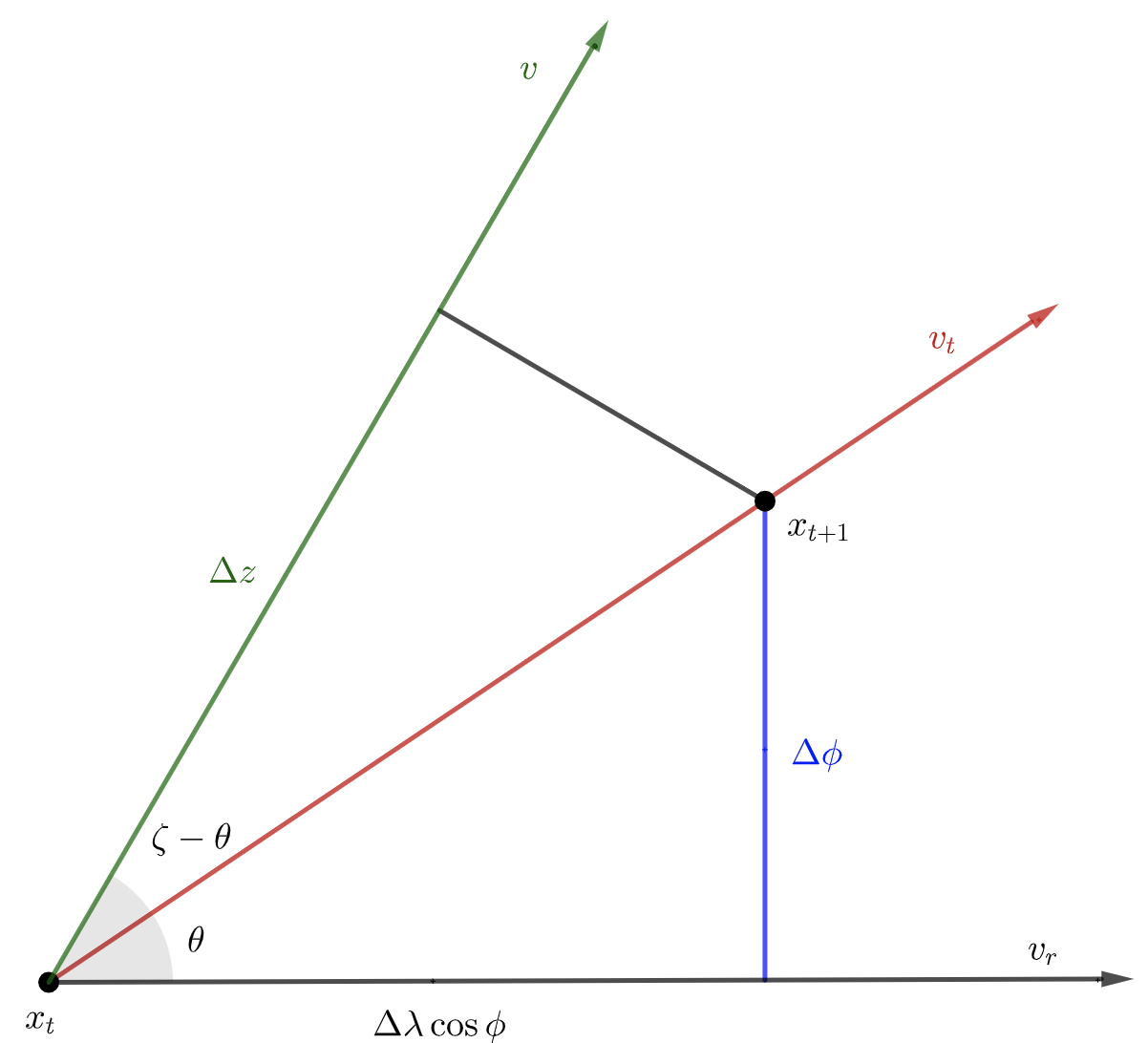
In the diagram, $x_t$ and $x_{t+1}$ represent two points in his trajectory that are close together. Note that $v$ always points at $\chi$, while $v_r$ always points in the horizontal direction. From the diagram, we can see how $\Delta z$ and $\Delta \lambda$ are related:

(j) (ques)

The zenith distance approaches its minimum value when the vectors $v$ and $v_t$ are perpendicular, since this indicates that it will no longer be possible for him to move closer to $\chi$ due to Earth’s rotation.

In other words, this happens when $\zeta - \theta = 90^{\circ}$. Substituting this into our expression from part (h),

which implies

Remark. Note that the condition $\zeta - \theta = 90^{\circ}$ agrees with the equation derived in part (i). As we approach the minimum zenith angle, the amount of horizontal distance needed to travel in order to change the zenith angle by a fixed $\Delta z$ effectively approaches infinity.

Section 3

(k) (ques)

In order for $\chi$ to be directly overhead, he needs to have the same declination and right ascension as $\chi$.

The amount of time he needs to increase his latitude to $\delta$ is bounded below by

which is when he travels straight north at all times.

On the other hand, the amount of time it takes him to have the same right ascension is bounded above by

which is when he travels straight west at all times. Since $4\alpha/3 < 4\delta$, he cannot get $\chi$ to his zenith when it first culminates.

(l) (ques)

From part (h), he cannot get $\chi$ directly overhead the first time it culminates. Therefore, his best strategy is to try to get $\chi$ to his zenith the next time it appears above his horizon. After time $t$, the change in his right ascension due to the rotation of the earth is $\omega t$. Therefore, to optimize his distance travelled, he should travel along a great circle (defined on the surface of the Earth) that increases his longitude by $(2\pi + \alpha - \omega t)$, and increases his latitude by $\delta$.

Let $N$ be the north celestial pole, and $Y$ be his stopping point, which has coordinates $(2\pi + \alpha-\omega t, \delta)$. Note that the coordinates of $Y$ are his longitude and latitude on Earth, and not in the celestial sphere. Also, $Y\gamma = \omega t/4$, since the maximum speed his boat can travel is $\omega R_{\oplus}/4$. Now, the spherical law of cosines in $\triangle{NY\gamma}$ gives

so

Now we can numerically iterate. Using $t = \text{20 hrs}$ as a first guess, we get $\omega t = 300.2^{\circ}$, which gives $(t-\text{20 hrs})\approx 48\text{ s}$. To account for approximation errors, a large range of values in this general vicinity are acceptable.